奥行距離の計算
四角形の4点を反時計回りにK1、K2、K3、K4とします。K1-K2が道路に平行と考えます。
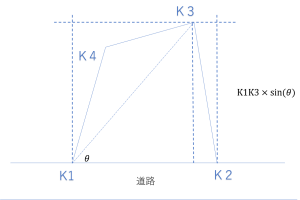
ここで、K1-K2間の距離は「間口距離」といいます。道路から最も遠い点はK3です。
そこで、K1の対角上の点K3をむすんだ線、K1ーK3を求め、これを極座標に変換します。
変換した結果、得られた2点間の距離r(K1K3 )と方向角θを用いて、r× sinθ を計算するとこれが「奥行距離」です。
簡単な例で計算してみましょう。座標を次のように与えます。
| 座標 | x | y |
| K1 | 56.00 | 53.00 |
| K2 | 56.00 | 85.00 |
| K3 | 25.00 | 81.00 |
| K4 | 18.00 | 54.00 |
K1ーK2のx座標を同じにしていますので、K1、K2は、X軸に対して垂直にならんでいます。また、間口距離(K1-K2)は、y座標を引き算して85-53=32mと計算できます。間口距離は32mです。
(1)最初に、K1-K3をつなぐ線分を極座標で表します。
関数電卓では、Pol( )を使います。
Pol(25-56, 81-53) = (r=41.77, θ = 137.91度)
よって、奥行距離は
41.77×sin(137.91) = 28m
これは、K1、K3のy座標の差、81-53=28 と一致します。
(2)次に、K2-K4をつなぐ線分を極座標で表します。
Pol(18-56, 54-85) = (r=49.04, θ =-140.79度)
よって、奥行距離は
49.04×sin(140.79) = 31m
こちらもK2、K4のy座標の差、85-54=31 と一致します。
28m < 31mなので、31mが奥行距離となります。
K4のほうが遠くにある点ということです。
間口距離は32m、奥行距離は31mでした。(想定整形地の面積は、32×31で求まります。)
